Ich habe in der Vergangenheit schon über die Herausforderungen beim Kombinieren von Mobile Mapping Daten geschrieben, worunter das Finden geeigneter Geometrie und die richtige Gewichtung der überlappenden Fahrten. Ein anderes Problem entsteht wo Fahrten verzweigen oder wieder zusammenkommen.
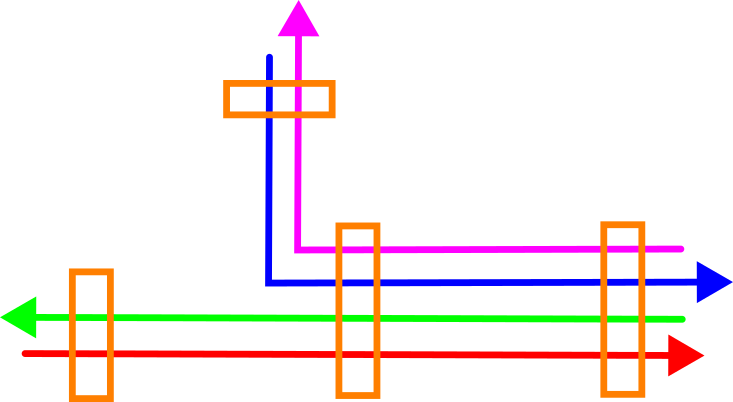
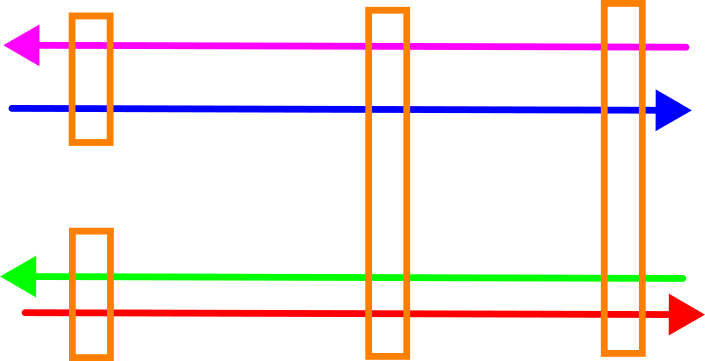
Untenstehende Abbildung zeigt die Oberansicht einer Beispielsituation mit vier Fahrten die an vier Stellen miteinander kombiniert werden. An zwei Stellen überlappen sie alle und können gemeinsam ausgeglichen werden, aber an den zwei anderen Stellen überlappen jeweils nur zwei Fahrten.
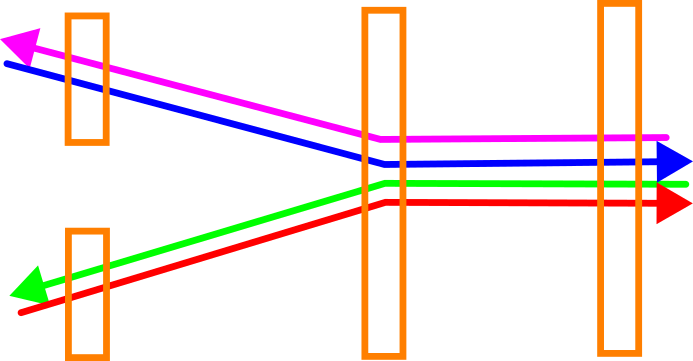
Untenstehende Abbildung zeigt eine Seitenansicht dieser Situation. Die magentafarbene und blauwe Fahrt liegen nahe beieinander, die rote und grüne auch – aber zwischen diesen zwei Paaren gibt es eine systematische Abweichung. Das kommt in der Praxis oft vor, vor allem wenn die Fahrten zu verschillenden Zeiten stattgefunden haben.
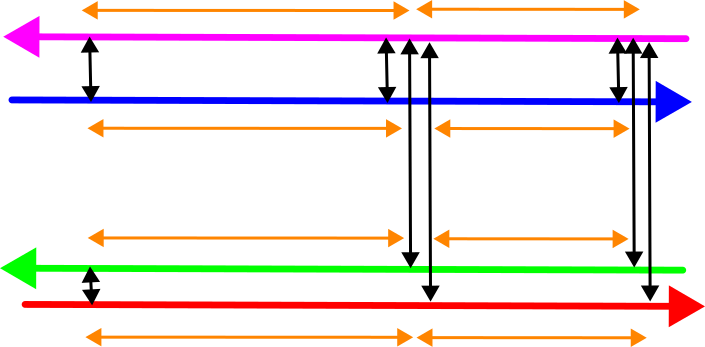
Die Differenzen zwischen den Fahrten (schwarze Pfeile) können mit einer geeigneten Methode bestimmt werden, wonach Korrekturwerte berechnet werden können die die Fahrten aufeinander fallen lassen. Meine HaiQuality Adjust Software vergleicht dabei die berechneten Korrekturen mit dem a-priori stochastischen Modell und passt dieses wo nötig an um die richtige Gewichtung der verschieden Fahren zu erhalten. Hierdurch wird verhindert, dass Fahrten von schlechter Qualität das Gesamtergebnis negativ beeinflussen.
Wenn jede Stelle einzeln betrachtet wird können Verzweigungen in den Fahrten leider zu Verformungen der Daten führen. Im Fall unseres Beispiels werden die Fahrten „geknickt“ und divergieren jenseits der gemeinsamen Ausgleichungsstellen schnell.
Die Lösung hierfür ist das Hinzunehmen neuer Beobachtungen (die orangefarbenen Pfeile) die die Stellen miteinander verbinden:
Es ergeben sich also die folgenden Beobachtungen:
- Die Differenzen zwischen den Fahrten bei jeder Ausgleichungsstelle. Diese erhalten ein großes Gewicht um sicherzustellen, dass die Punktwolken hier exakt aufeinander eingepasst werden.
- De Verbindungen zwischen den Ausgleichungsstellen. Diese haben den Wert 0 (keine Differenz), aber ein niedrigeres Gewicht das von der Genauigkeit des jeweiligen Bahnstücks abhängig sein muss.
Unsere Unbekannten sind die Korrekturen jeder Ausgleichungsepoche, also eine Unbekannte pro Ausgleichungsstelle und Fahrt.
Es ergibt sich ein Netz das in einem Gauss-Markov-Modell ausgelichen werden kann. Das funktionale Modell ist sehr einfach und linear, die Designmatrix enthält nur die Werte -1 und 1 – wie bei einem Nivellement. Ohne Anschlusspunkte ist die Normalgleichungsmatrix unterbestimmt, darum wird die Moore-Penrose Pseudoinverse benützt um die ausgeglichenen Parameter zu berechnen. Auch hier kann iteratief das stochastische Modell verfeinert werden. Dabei ist es noch nicht mal nötig, die Verbesserungen zu berechnen, da die berechneten Korrekturen direkt Auskunft über die Genauigkeit der Fahrten liefern.
Theoretisch soweit alles gut, aber wie sieht es in der Praxis aus? Als Beispiel habe ich hier ein Gleisvermessungsprojekt. Die Datenaufnahme fand an drei Tagen unter schwierigen Bedingungen statt (niedrige Geschwindigkeit, relativ lange Basislinien, hohe ionosphärische Aktivität, Stillstand an überdachten Bahnsteigen mit sehr schlechtem GNSS Empfang), wobei fast 30 Fahrten erforderlich waren um das Projektgebiet vollständig zu bedecken. Hierdurch ergaben sich für manche Fahrten recht große Korrekturen. Der Gleisplan ist komplex, einschließlich eines Rangierbahnhofs, wodurch mehrere Stelle entstanden an denen Gleise und damit Fahrten verzweigen und nicht mehr überlappen.
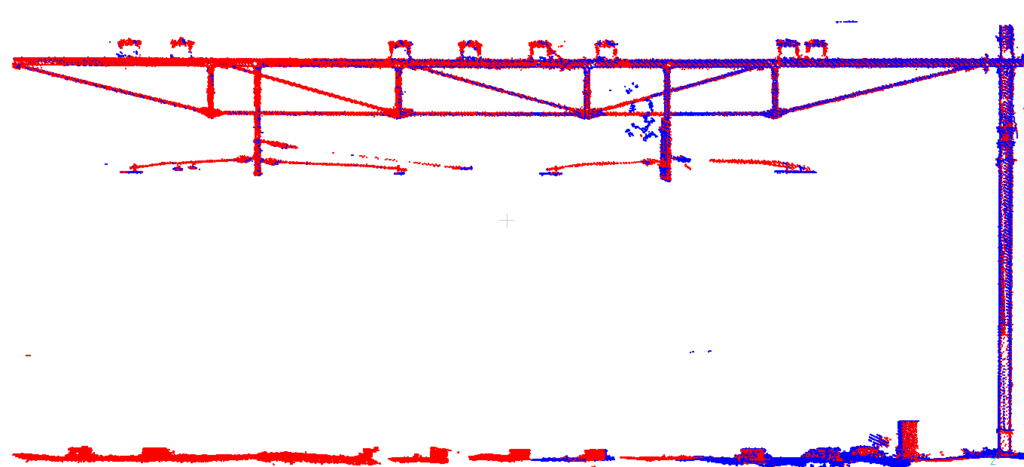
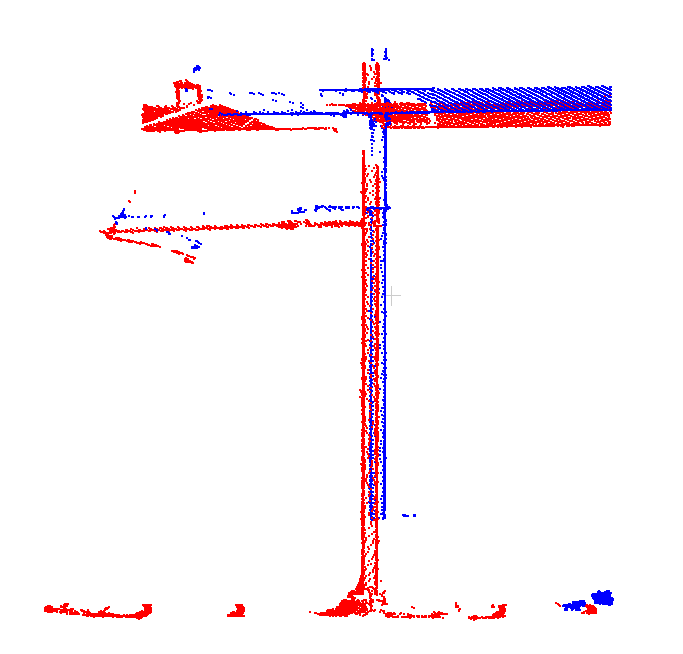
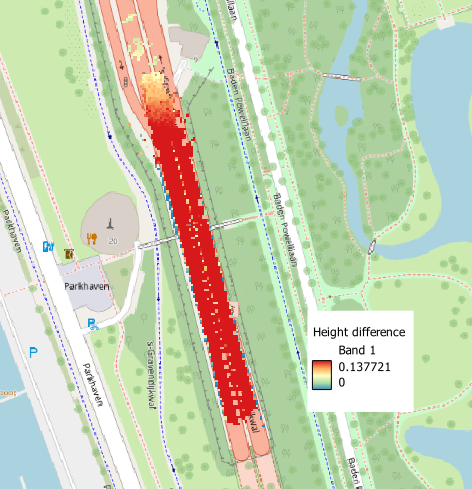
Schauen wir uns erst den „alten“ Ansatz an der jede Stelle einzeln ausgleicht. Hier der Plot der Punktwolken zweier Fahrten nach gemeinsamer Ausgleichung:
Und hier etwas weiter, nicht mehr gemeinsam ausgeglichen da kaum Überlappung. Die zwei Fahrten liegen schon nicht mehr gut aufeinander:
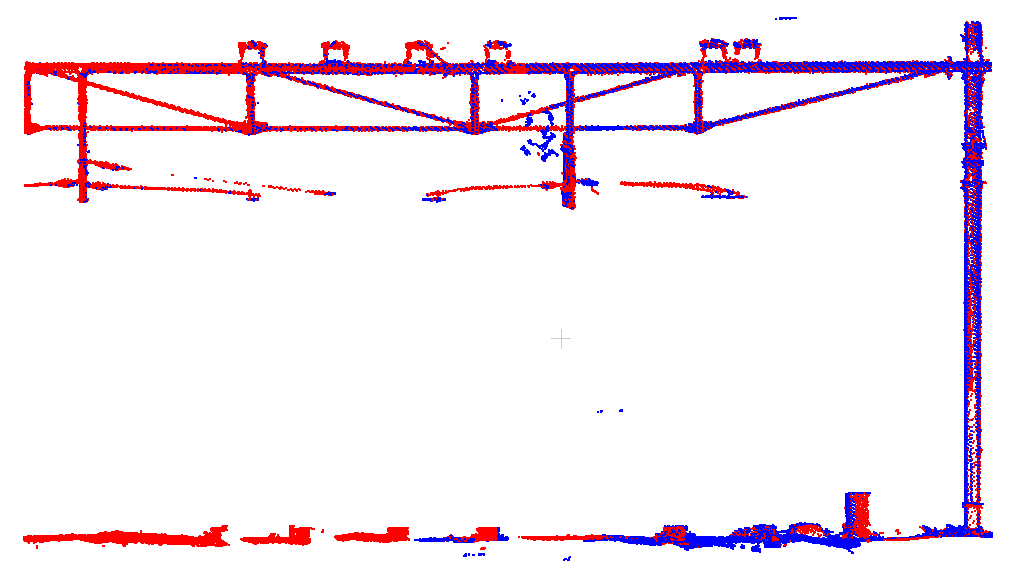
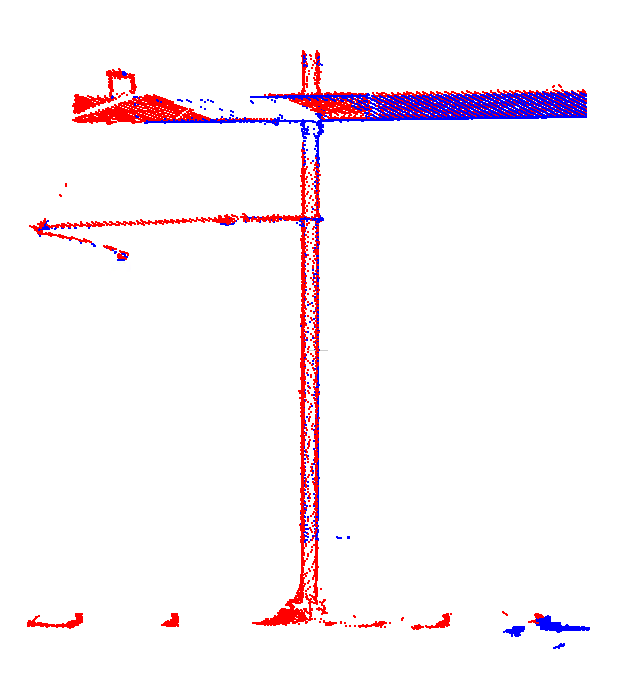
Hier ist die erste Stelle wie sie aus der neuen Ausgleichungsmethode folgt. Wiederum liegen beide Fahrten gut aufeinander:
Und hier ist die zweite Stelle. Obwohl die beiden Fahrten nicht Mitglied der gleichen Stelle sind und damit keine direkten Differenzen bestimmt wurden, sorgt die vollständige Netzausgleichung dafür, dass auch hier die Fahrten gut aufeinder liegen:
Das Schöne an diesem Ansatz ist, dass er keine Mehrarbeiten mit sich bringt. Es ist noch immer ausreichend, die Differenzen zwischen überlappenden Fahrten zu bestimmen. Bessere Qualität ohne Mehrarbeit, was will man mehr?