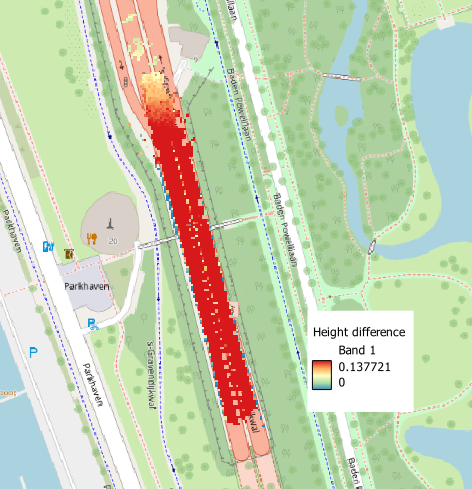
Ik heb eerder over de uitdagingen van het vereffenen van Mobile Mapping data geschreven, waaronder het vinden van geschikte geometrie en de juiste weging van de overlappende ritten. Een ander probleem ontstaat waar ritten vertakken of weer bij elkaar komen.
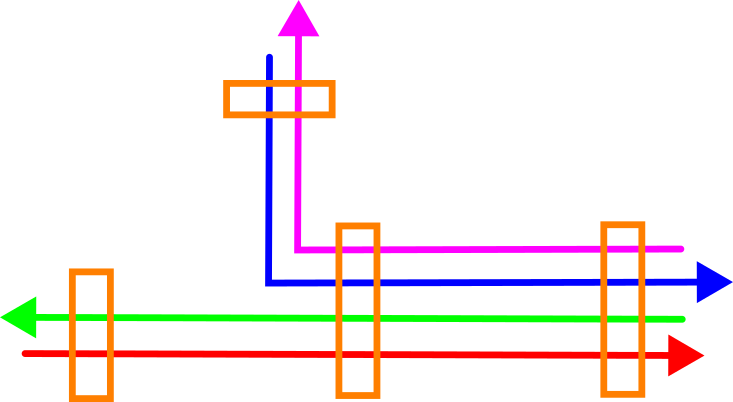
Onderstaande afbeelding toont een bovenaanzicht van een voorbeeldsituatie met vier ritten die op vier locaties met elkaar vereffend worden. Op twee locaties overlappen alle vier en kunnen met elkaar vereffend worden, maar bij de twee anderen overlappen er telkens slechts twee.
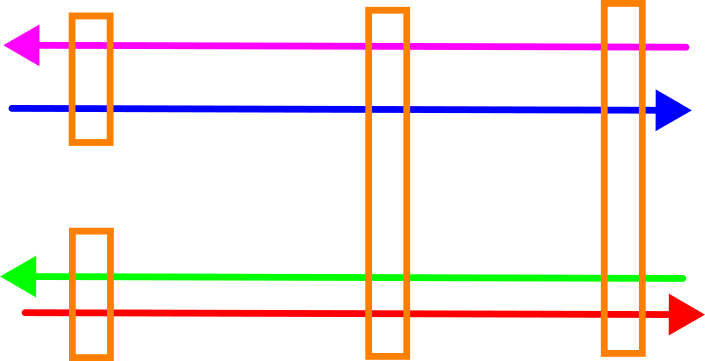
Onderstaande afbeelding toont een zijaanzicht van deze situatie. De paarse en blauwe rit liggen dicht bij elkaar, net als de rode en de groene – maar er is een stelselmatige offset tussen deze twee paren. Dit komt vaker voor, vooral als de ritten in verschillende sessies en dus op verschillende momenten zijn ingewonnen.
De verschillen tussen de ritten (zwarte pijlen) kunnen met een geschikte methode bepaald worden, waarna correcties berekend kunnen worden die de ritten op elkaar laten vallen. Mijn HaiQuality Adjust software vergelijkt de correcties met het a-priori kansmodel en past dit waar nodig aan om zo de juiste weging van de verschillende ritten te verkrijgen. Hierdoor wordt voorkomen dat ritten van lage kwaliteit de totale oplossing verstoren.
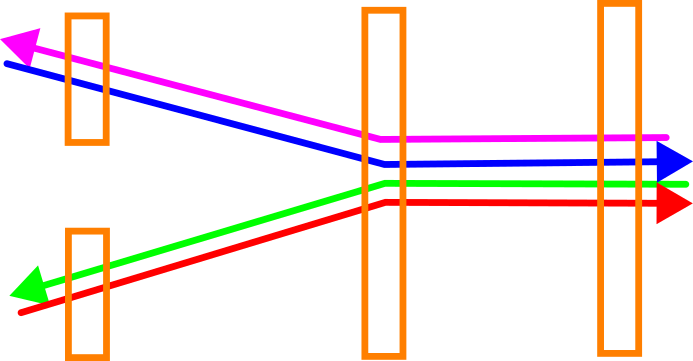
Als elke locatie apart beschouwd wordt kunnen aftakkingen in de ritten helaas tot vervormingen in de data leiden. In het geval van ons voorbeeld worden de ritten “geknikt” en lopen voorbij de gezamenlijke vereffeningslocatie snel uit elkaar.
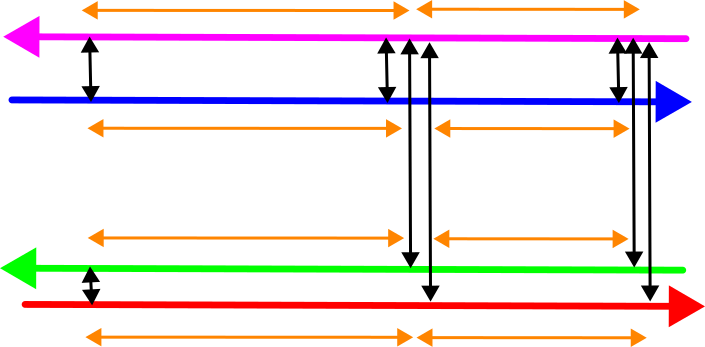
Dit kan opgelost worden door aanvullende waarnemingen (de oranje pijlen) toe te voegen die de locaties met elkaar verbinden:
Hieruit resulteren dus de volgende waarnemingen:
- De verschillen tussen de ritten bij elke vereffeningslocatie. Deze krijgen een groot gewicht om te borgen dat de puntenwolken hier exact op elkaar gerekend worden.
- De verbindingen tussen de vereffeningslocaties. Deze waarnemingen hebben als waarde 0 (geen verschil), maar een lager gewicht dat afhankelijk dient te zijn van de nauwkeurigheid van het desbetreffende stuk van de rit.
Onze onbekenden zijn die correcties van elke vereffeningsepoche, dus één onbekende voor elke vereffeningslocatie en rit.
Het resultaat is een netwerk dat met de kleinste-kwadraten-methode in een A-model vereffend kan worden. Het functionele model is zeer eenvoudig en lineair en bevat in de designmatrix slechts de waarden -1 en 1 – net als bij een waterpassingsnetwerk. Zonder paspunten is de normaalvergelijkingsmatrix slecht geconditioneerd, dus wordt de Moore-Penrose pseudoinverse gebruikt om de vereffende parameters te berekenen. Wederom kan door iteratieve herweging het kansmodel verfijnd worden. Hiervoor hoeven nog niet eens de residuen berekend te worden doordat de berekende correcties direct informatie leveren over de (on)nauwkeurigheid van de ritten.
Zover dus de theorie, maar werkt het in de praktijk? Als voorbeeld heb ik hier een spoorproject. De inwinning vond plaats onder uitdagende omstandigheden (lage snelheden, relatief lange basislijnen, hoge ionosferische activiteit, stilstand onder perronkappen met zeer slecht GNSS ontvangst) gedurende drie dagen, met bijna 30 ritten die voor volledige scopedekking vereffend moesten worden. Dit resulteerde in relatief grote correcties voor sommige ritten. Het sporenlayout is complex inclusief een emplacement, waardoor er meerdere locaties ontstonden waar sporen en dus ritten uit elkaar gaan en niet meer overlappen.
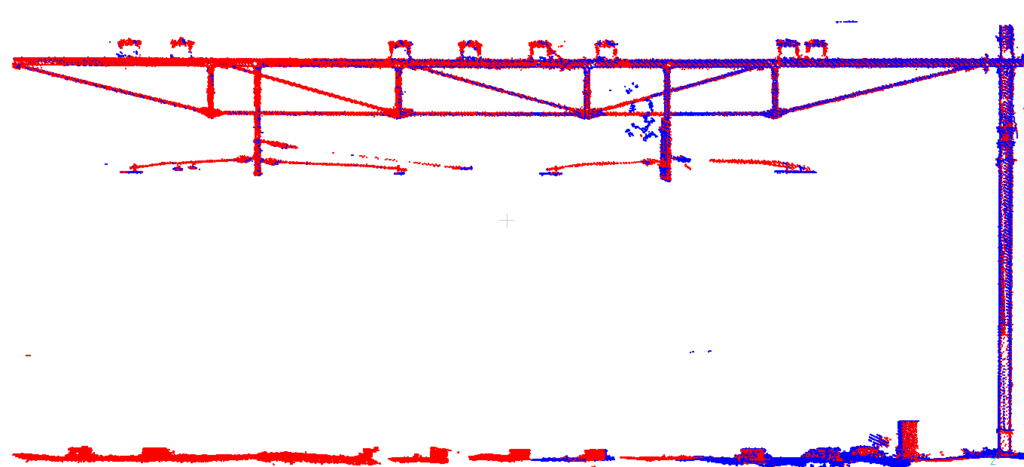
Laten we eerst naar de “oude” aanpak kijken die elke locatie apart vereffend. Hier is een plot van de puntenwolken van twee ritten na vereffening bij een gezamenlijke locatie:
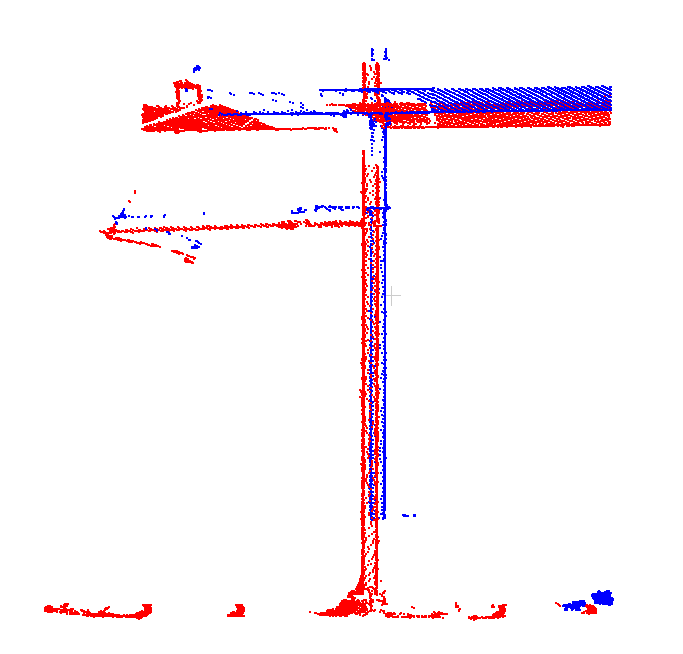
En hier een stuk verderop, niet meer gezamenlijk vereffend omdat er nauwelijks overlap is. De twee ritten liggen hier al niet meer goed op elkaar:
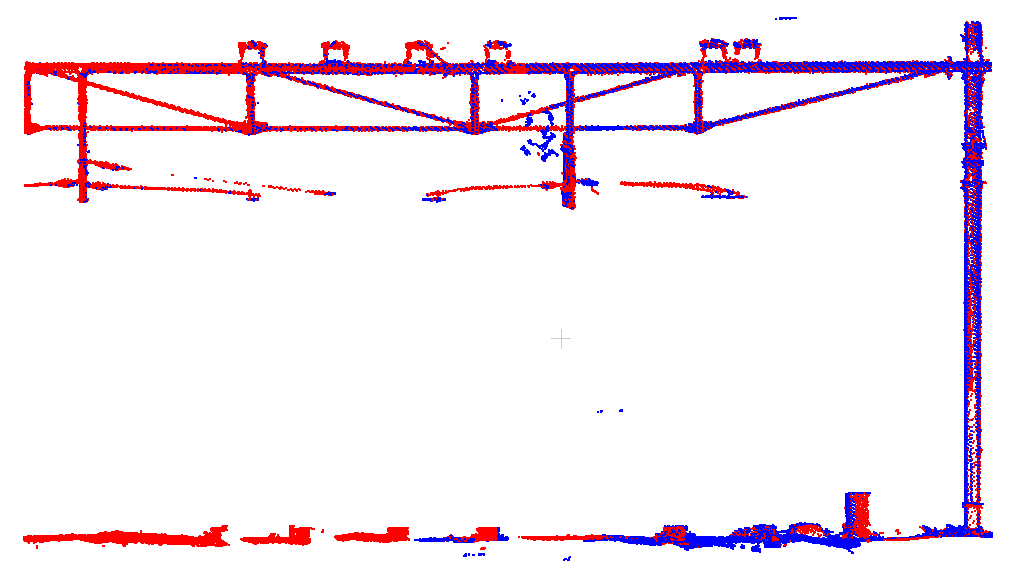
Hier is de eerste locatie zoals deze volgt uit de correcties die met de nieuwe vereffeningsmethode zijn berekend. Wederom liggen beide ritten goed op elkaar:
En hier is de tweede plek. Ondanks dat de ritten hier niet gezamenlijk zijn vereffend, dus geen directe verschillen tussen deze ritten berekend zijn, zorgt de volledige netwerkvereffening ervoor dat de ritten goed op elkaar liggen:
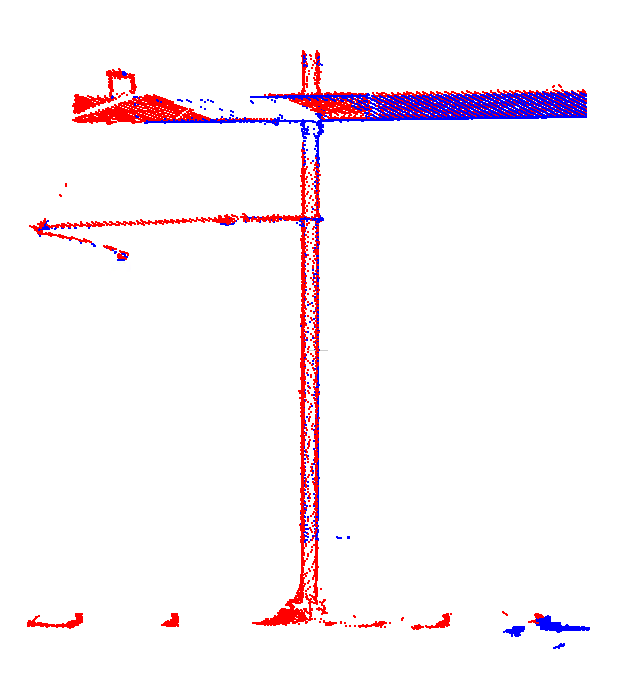Het mooie is dat deze nieuwe methode geen meerwerk met zich meebrengt. Nog steeds hoeven alleen maar de verschillen tussen overlappende ritten berekend te worden. Betere kwaliteit zonder meerwerk, wat wil je meer?
